🔑 대표적 그래프(Graph) 탐색 알고리즘인 DFS/BFS를 소개합니다.

그래프(Graph)는 뭘까?

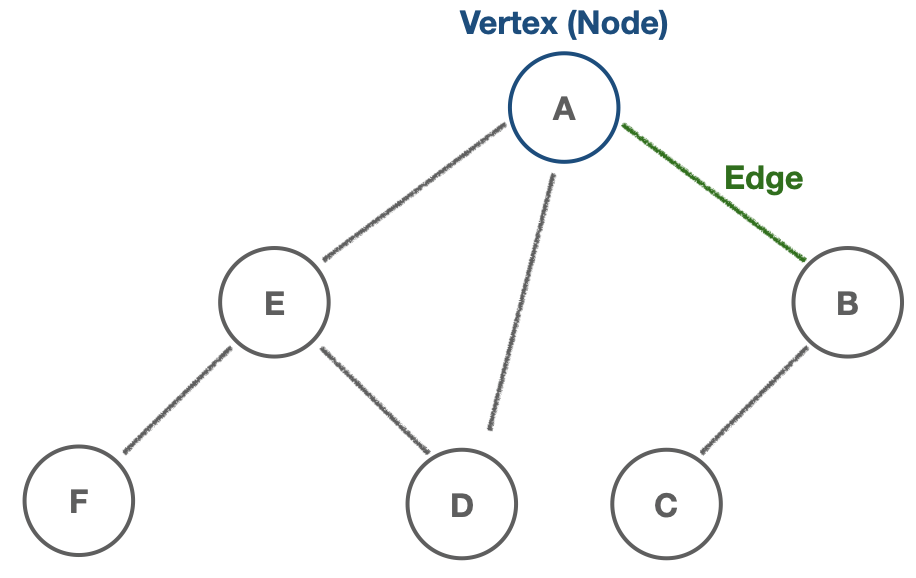
• 그래프(Graph) 는 정점(vertex, 노드)과 간선(edge)로 구성된 유한한(finite) 자료구조 입니다.
• 두 정점(노드)가 간선으로 연결되면 '두 노드는 인접(Adjacent)하다' 라고 합니다.

• 페이스북, 인스타그램 같은 소셜 네트워크의 데이터베이스가 그래프 구조로 만들어져 있습니다. 그래프 구조를 통해 사람들(node) 사이의 관계(edge) 를 쉽게 탐색할 수 있습니다.

그래프 탐색

• 하나의 정점(노드)에서 모든 노드를 한 번씩 탐색(방문) 하는 것을 말합니다.

DFS(Depth-First Search, 깊이 우선 탐색)

• 그래프의 최대 깊이까지 탐색한 후, 다른 경로로 이동하여 탐색하는 알고리즘입니다.

  • 시작 노드에서 최대한 멀리 있는 노드 를 우선 탐색합니다.

• DFS를 활용하여 미로찾기 문제를 해결할 수 있습니다. 미로 속의 길을 간선(edge)으로, 막다른 지점을 정점(node)으로 보고 미로의 도착점에 도달할 때까지 각 경로의 최대 깊이까지 탐색합니다. 현재 선택한 경로가 막다른 골목에 부딪히면 되돌아가서(백트래킹) 다른 경로를 탐색합니다.

• DFS를 활용하여 미로찾기 문제를 해결할 수 있습니다. 미로 속의 길을 간선(edge)으로, 막다른 지점을 정점(node)으로 보고 미로의 도착점에 도달할 때까지 각 경로의 최대 깊이까지 탐색합니다. 현재 선택한 경로가 막다른 골목에 부딪히면 되돌아가서(백트래킹) 다른 경로를 탐색합니다.

• 스택과 재귀함수를 이용하여 구현할 수 있습니다.

  • DFS 구현 예시

    const result = []; // 결과 배열
    const visited = {}; // 방문한 노드 체크
    
    const = dfs => (graph, node) {
      // 정점이 빈 값이면 null을 반환
      if (!node) return null;
      // 현재 노드를 방문 처리
      visited[node] = true;
      // 결과 배열에 노드 추가
      result.push(node);
      // 현재 노드의 인접 노드 방문 처리(재귀)
      graph[node].forEach((v) => {
        if (!visited[v]) dfs(v);
      });
    }
    dfs(start);
    return result;
    

BFS(Breadth-First Search, 너비 우선 탐색)

• 그래프의 근접 노드부터 탐색한 후, 다른 경로로 이동하여 탐색하는 알고리즘입니다.

  • 시작 노드에서 최대한 가까운 노드(이웃 노드) 부터 우선 탐색합니다.

• BFS는 P2P 파일 네트워크에서 피어(peer) 노드를 탐색할 때 활용할 수 있습니다. BFS를 활용해 가장 가까운 이웃 노드만 빠르게 탐색할 수 있습니다.

• 큐를 이용하여 구현할 수 있습니다.

  • BFS 구현 예시

    const bfs = (graph, start) => {
      const queue = [start],
        visited = {},
        result = [];
      let node; // 탐색할 현재 노드
      // 현재 노드를 방문 처리
      visited[start] = true;
      // 큐가 비어있을 때까지 반복
      while (queue.length) {
        node = queue.shift();
        result.push(node);
        // 현재 노드의 방문 안 한 인접 노드 큐에 추가
        for (let v of graph[node]) {
          if (!visited[v]) {
            visited[v] = true;
            queue.push(v);
          }
        }
      }
      return result;
    };
    bfs(start);
    

※ Big-O

• 시간 복잡도는 두 탐색 알고리즘 모두 O(N) (N: 그래프 노드의 개수) 입니다.

• 공간 복잡도는 DFS보다 BFS 상대적으로 큽니다.(더 많은 메모리 차지)

💡정리

• DFS는 그래프의 깊이를 우선으로 탐색하고, 스택과 재귀를 통해 구현할 수 있습니다.(백트래킹)

• BFS는 그래프의 넓이를 우선으로 탐색하고, 큐를 통해 구현할 수 있습니다. (최적해)

• BFS는 탐색해야 할 그래프의 깊이가 노드마다 다르거나 단일 대답이 필요한 경우((예)최단 경로 구하기 등)에 유리합니다.

• 그래프의 모든 노드를 탐색해야 한다면 DFS가 더 좋은 방법일 수 있습니다.

🔗Reference

Graph | AWS

Graphs: breadth-first search | freeCodeCamp

Graphs: depth-first search | brilliant

Algorithm Visualizer

DFS와 BFS의 차이

BFS로 최단거리 찾기 | freeCodeCamp

p2p-file-sharing | geeksforgeeks